| Version 1 (modified by , 4 years ago) ( diff ) |
|---|
Overview of the Analysis Step for 3D-Var Methods
PDAF-OMI Guide
Implementation Guide
The 3D-Var methods were added in PDAF V2.0.
For the analysis step of ensemble filters several routines need to be implemented. We prove a conceptional overview here. The detailed interfaces are then described on the following pages.
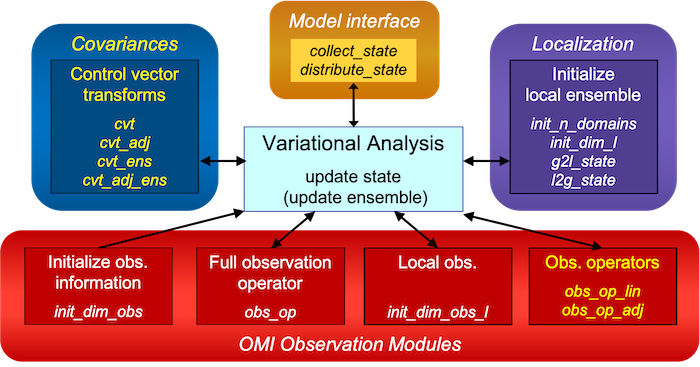
Figure 1: Required routines for the analysis step of 3D-Var methods. There are four groups of routines: The interface to the model (orange), the observation module (red), state localization in case of Ensemble or Hybrid Var using the LESTKF (purple), and handling of covariances (blue). The routine marked in yellow are additions compared to what is required for ensemble filters.
Figure 1 gives an overview of the different routines that might need to be provided to the analysis step of an a 3D-Var method. The actual routines depend on the chosen 3D-Var method as wil be described after discussing the groups of subroutines.
The routines are organized in four groups:
Model Interface
The model Interface consists of the routines
collect_state_pdafanddistribute_state_pdaf. These routine perform the concersion between model fields and state vector. The routines have been discussed in the context of the modification of the model for the ensemble integration.
OMI Observation Module
The observation module performs all observation-related operations. In case of OMI, one needs the following routines:
init_dim_obs_pdafomi: For each observation type that is assimilation this routine reads the observations and initialized observation values, coordinates, and errors. In addition indices are specified that link the state vector to the observations so that the observation operator is preparedobs_op_pdafomi: For each observation type there is one routine providing the observation operator. For this, OMI provides different observation operatorsinit_dim_obs_l_pdafomi: This routine initializes the local observations of each observation type. This is only required if the LESTKF is applied to transform the ensemble perturbations. With OMI this is mainly a single subroutine call, while OMI does the actual initializationobs_op_lin_pdafomi: This routine applied the linearized observation operator for each observation type during the iterative optimization. So far OMI only provised linear observation operators. For theseobs_op_lin_pdafomican call the same operator atobs_op_pdafomi.obs_op_adj_pdafomi: This routine applied for each observation type the adjoint observation operator. This is applied to the observation vector and returns a state vector. OMI provides the adjoints of the provided forward operators.
Localization
These routines are only required for 3D-Var variants transforming the ensemble perturbations with the LESTKF. They handle the initialization of the state vector for a local analysis. These routines are
init_n_domain: This routine sets the number of local analysis domainsinit_dim_l: This routine determines the state vector size for the local analysis domain and initializes the index information to fill a local state vectorg2l_state: This routine performs the transformation from a global to the local state vector. It selects elements of the global state vector and fill the local vectorl2g_state: This routine performns the back-ttransformation from local to global state vector.
Covariances
The covariance routines perform the so-called control vector transformation (cvt). The 3D-Vars are implemented in incremental form and transform from the state space (state vector increment dx) to the control space (control vector v) using a square-root L of the background covariance matrix B = L LT.
cvt_pdaf: This routine performs the transformation x = L v.cvt_adj_pdaf: This routine performsn the adjoint transformation y = L xcvt_ens_pdaf: This routine performs the transformation x = Z v using an ensemble-represented matrix square root Z with Z ZT = B. For this operation the routine is provided with the array holding the state ensemble.cvt_adj_ens_pdaf: This routine performsn the adjoint transformation y = Z x using an ensemble-represented matrix square root Z with Z ZT = B. For this operation the routine is provided with the array holding the state ensemble.
3D-Var Methods in PDAF
PDAF provides 3 different variants of 3D-Var. For those methods using en ensemble to represent covariances, the transformation of ensemble perturbations can be cmoputed using the global ESTKF or the localized LESTKF filters. The methods are
- 3D-Var: This variant uses parameterized covariances. It is run in PDAF with an ensemble size of one. The functionality in
cvt_pdafandcvt_adj_pdafis coded by the user according to the particular problem, e.g. by using variable transformations for balances or using decorrelation lengths or EOFs to propagate increments. - 3D Ensemble Var: The ensemble variational method represents the covariance by an ensemble. Thus the functionality in
cvt_ens_pdafandcvt_adj_ens_pdafis, in its simplest form, simply given by the scaled ensemble perturbations. In addition localization can be applied. In this case the number of columns of the ensemble array is multiplied and tapering is applied. The transformation of the ensemble transformations can be performed in two ways- ESTKF:: In this case the ensemble perturbations are transformed by the global ESTKF method. Adapt from using the ensemble variances of the cvt-routines, the interface for this 3D-Var method is identical to that of the parameterized 3D-Var.
- LESTKF:: In this case the ensemble perturbations are transformed by the local ESTKF method. In this case, the call to the assimilation routine also specifies the routines needed to apply the localization.
- Hybrid 3D-Var: The hybrid 3D-Var implementation represents the covariance matrix by a combination of a parameterized with an ensemble part. Thus mathematically the columns are concatenated as B1/2 = [L Z]. In practive this variant call both
cvt_pdafandcvt_ens_pdaf(and likewise both adjoint variants) one after the other and each routine does its part of the covariance operation. As for the 3D Ensemble Var, the transformation of the ensemble transformations can be performed in two ways- ESTKF:: In this case the ensemble perturbations are transformed by the global ESTKF method. Compared to the interface of the parameterized 3D-Var, the call to the assimilation routine includes all cvt routines, both for the parameterized and the ensemble transformatiob.
- LESTKF:: In this case the ensemble perturbations are transformed by the local ESTKF method. In this case, the call to the assimilation routine also specifies the routines needed to apply the localization.
Note on 3D Ensemble Var vs. Hybrid 3D-Var: The hybrid 3D-Var implemented provides a clear separation between the parameterized and the ensemble parts, which should make the combined use easy. However, this scheme might be to restrictive depending on how one likes to combine the ensemble information with the parameterized covariance operations. To this end one can base a more advanced hybrid implementation on 3D Ensemble Var variant. In particular it is important to note that the routines cvt_ens_pdaf and cvt_adj_ens_pdaf are not restricted to using the ensemble-represented covariances. Also the dimension of the control vector can be freely specified and is not restrictired to a multiple of the ensemble size. This allows to apply any combination of parameterized and ensemble covariance operation.
Code examples
The different 3D-Var variants are demonstrated in the tutorial code in the PDAF package in the sub-directories of
tutorial/variational/
These tutorial implementations are analogous to the tutorials for the ensemble filters.
Documention of the required implementations
For the application of the 3D-Var methods there are separate routines (added with PDAF 2.0):
