Overview of the Analysis Step for 3D-Var Methods (PDAF2)

The 3D-Var methods were added in PDAF V2.0.

For the analysis step of ensemble filters several routines need to be implemented. We prove a conceptional overview here. The detailed interfaces are then described on the following pages.

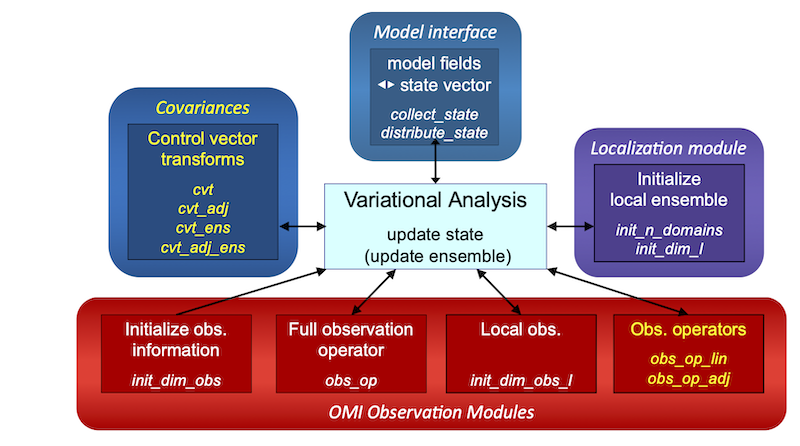
Figure 1: Required routines for the analysis step of 3D-Var methods. There are four groups of routines: The interface to the model (orange), the observation module (red), state localization in case of Ensemble or Hybrid Var using the LESTKF (purple), and handling of covariances (blue). The routine marked in yellow are additions compared to what is required for ensemble filters. Without PDAFlocal there are two additional routines in the localization module.

Figure 1 gives an overview of the different routines that might need to be provided to the analysis step of an a 3D-Var method. The actual routines depend on the chosen 3D-Var method as wil be described after discussing the groups of subroutines.

The routines are organized in four groups:

Model Interface

The model Interface consists of the routines collect_state_pdaf and distribute_state_pdaf. These routine perform the concersion between model fields and state vector. The routines have been discussed in the context of the modification of the model for the ensemble integration.

OMI Observation Modules

The observation modules perform all observation-related operations. There is one observation module per observation type. The call-back routines are collected in the file callback_obs_pdafomi.F90. Each of these routines then calls a subroutine in the observation model specific to the observation type.

Relevant for 3D-Var methods callback_obs_pdafomi.F90 has to contain the routines:

• init_dim_obs_pdafomi:
  For each observation type that is assimilated, this routine calls a routine form the observation modules that reads the observations and initializes observation values, coordinates, and errors. In addition, indices are specified that link the state vector to the observations. These are used in the observation operator.
• obs_op_pdafomi:
  For each observation type, there is one routine providing the observation operator. For this, PDAF-OMI provides different observation operators as subroutines.
• init_dim_obs_l_pdafomi:
  This is only used for the domain-localized in case of the 3D Ensemble-Var or hybrid ensemble Var using the LESTKF for ensemble transformation. It calls the observation modules to initialize the local observations of each observation type. With PDAF-OMI this is mainly a single subroutine call, while PDAF-OMI does the actual initialization.
• obs_op_lin_pdafomi: This routine applies the linearized observation operator for each observation type during the iterative optimization of the 3D-Var methods. So far PDAF-OMI only provides linear observation operators. For these obs_op_lin_pdafomi can call the same operator as for obs_op_pdafomi.
• obs_op_adj_pdafomi: This routine applies the adjoint observation operator for each observation type during the iterative optimization of the 3D-Var methods. This is applied to the observation vector and returns a state vector. OMI provides the adjoints of the provided forward operators.

Localization module

These routines are only required for 3D-Var variants transforming the ensemble perturbations with the LESTKF. They handle the initialization of the state vector for a local analysis. These routines are

• init_n_domain: This routine sets the number of local analysis domains
• init_dim_l: This routine determines the state vector size for the local analysis domain and initializes the index information to fill a local state vector

Covariances

The covariance routines perform the so-called control vector transformation (cvt). The 3D-Vars are implemented in incremental form and transform from the state space (state vector increment dx) to the control space (control vector v) using a square-root L of the background covariance matrix B = L L^T.

• cvt_pdaf: This routine performs the transformation x = L v. It is used in the parameterized 3D-Var and the hybrid 3D-Var methods.
• cvt_adj_pdaf: This routine performs the adjoint transformation y = L^T x. It is used in the parameterized 3D-Var and the hybrid 3D-Var methods.
• cvt_ens_pdaf: This routine performs the transformation x = Z v using an ensemble-represented matrix square root Z with Z Z^T = B. For this operation the routine is provided with the array holding the state ensemble. It is used in the 3D Ensemble Var and the hybrid 3D-Var methods.
• cvt_adj_ens_pdaf: This routine performsn the adjoint transformation y = Z^T x using an ensemble-represented matrix square root Z with Z Z^T = B. For this operation the routine is provided with the array holding the state ensemble. It is used in the 3D Ensemble Var and the hybrid 3D-Var methods.

3D-Var Methods in PDAF

PDAF provides 3 different variants of 3D-Var. For those methods using an ensemble to represent covariances, the transformation of ensemble perturbations can be computed using the global ESTKF or the localized LESTKF filters. The methods are

• 3D-Var:
  This variant uses parameterized covariances. It is run in PDAF with an ensemble size of one. The functionality in cvt_pdaf and cvt_adj_pdaf is coded by the user according to the particular problem, e.g. by using variable transformations for balances or using decorrelation lengths or EOFs to propagate increments.
• 3D Ensemble Var:
  The ensemble variational method represents the covariance by an ensemble. Thus, the functionality in cvt_ens_pdaf and cvt_adj_ens_pdaf is, in its simplest form, simply given by the ensemble perturbations divided by the ensemble size minus 1. In addition, localization can be applied. In this case the number of columns of the ensemble array is multiplied and tapering is applied to each group of columns. The transformation of the ensemble perturbations can be performed in two ways:
  • ESTKF:: In this case, the global ESTKF method transforms the ensemble perturbations. No localization is applied in this case.
  • LESTKF:: In this case, the local LESTKF method transforms the ensemble perturbations.
• Hybrid 3D-Var:
  The hybrid 3D-Var implementation represents the covariance matrix by a combination of a parameterized with an ensemble part. Thus mathematically the columns are concatenated as B^1/2 = [L Z]. In practice this variant calls both cvt_pdaf and cvt_ens_pdaf (and likewise both adjoint variants) one after the other and each routine does its part of the covariance operation. As for the 3D Ensemble Var, the transformation of the ensemble transformations can be performed in two ways:
  • ESTKF:: In this case, the global ESTKF method transforms the ensemble perturbations. No localization is applied in this case.
  • LESTKF:: In this case, the local LESTKF method transforms the ensemble perturbations.

Note on 3D Ensemble Var vs. Hybrid 3D-Var: The hybrid 3D-Var implemented provides a clear separation between the parameterized and the ensemble parts, which should make the combined use easy. However, this scheme might be too restrictive depending on how one likes to combine the ensemble information with the parameterized covariance operations. For more flexibility, one can base a more advanced hybrid implementation on the 3D Ensemble Var variant. In fact, the routines cvt_ens_pdaf and cvt_adj_ens_pdaf are not restricted to using the ensemble-represented covariances, but one can also include a parameterized component. Also, the dimension of the control vector can be freely specified and is not restrictired to a multiple of the ensemble size. This allows to apply any combination of parameterized and ensemble covariance operation.

Code examples

The different 3D-Var variants are demonstrated in the tutorial code in the PDAF package in the sub-directories of

   tutorial/3dvar/

These tutorial implementations are analogous to the tutorials for the ensemble filters.

Documention of the required implementations

For the application of the 3D-Var methods there are separate routines (added with PDAF 2.0):

• Implementation of the analysis for 3D-Var with parameterized background covariance matrix
• Implementation of the analysis for 3D Ensemble Var
• Implementation of the analysis for hybrid 3D-Var