Modification of the model code for the ensemble integration

Overview

Numerical models are typically implemented for normal integration of some initial state. For the data assimilation with a filter algorithm, an ensemble of model states has to be integrated for limited time until observations are available and an analysis step of the filter is computed. Subsequently, the updated ensemble has to be integrated further. To allow for the interruption of the integrations by the analysis step, the model code has to be extended. As described on the page on the implementation concept of the online mode, there are two options for the ensemble integration:

• fully parallel: For this implementation one needs to use a parallel computed with a sufficient number of processes such that the data assimilation program run be run with a concurrent time stepping of all ensemble states. Thus, if one runs each mode task with n processes and the ensemble has m members, the program has to run with n times m processes. This parallelism allows for a simplified implementation as each model task integrated only one model state and the model is always going forward in time.
• flexible: This variant allows to run the assimilation program in a way so that a model task (set of processors running one model integration) can propagate several ensemble states successively. In the extreme case, this could mean that one only a a single model task that is successively performing the integration of all ensemble states. The implementation for this variant is a bit more complicated, because one has to ensure that the model can jump back in time.

The extension to the model code for both cases is depicted in the figure below (See also the page on the [ImplementationConceptOnline implementation concept of the online mode.)

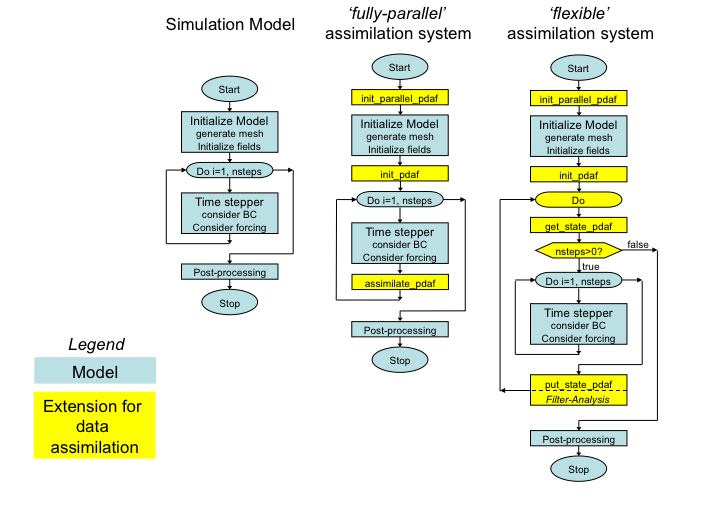
Figure 1: (left) Generic structure of a model code, (center) extension for fully-parallel data assimilation system with PDAF, (right) extension for flexible data assimilation system with PDAF.

Operations that are specific to the model and to the assimilated observations are performed by call-back routines that are supplied by the user. These are called through the defined interface of PDAF. Generally, these user-supplied routines have to provide quite elementary operations, like initializing a model state vector for PDAF from model fields or providing the vector of observations. PDAF provides examples for these routines and templates that can be used as the basis for the implementation. As only the interface of these routines is specified, the user can implement the routines like a routine of the model. Thus, the implementation of these routines should not be difficult.

PDAF_get_state

The routine PDAF_get_state has the purpose to initialize the information, whether further model integrations have to be computed and how many time steps have to be performed. In addition, the model fields to be propagated are initialized from the array holding the ensemble states.

The interface of PDAF_get_state is the following:

  SUBROUTINE PDAF_get_state(nsteps, timenow, doexit, U_next_observation, U_distribute_state, &
                            U_prepoststep, status)

with the following arguments:

• nsteps: An integer specifying upon exit the number of time steps to be performed
• timenow: A real specifying upon exit the current model time.
• doexit: An integer variable defining whether the assimilation process is completed and the program should exit the while loop. For compatibility 1 should be used for exit, 0 for continuing in the loop.
• U_next_observation: The name of a user supplied routine that initializes the variables nsteps, timenow, and doexit
• U_distribute_state: The name of a user supplied routine that initializes the model fields from the array holding the ensemble of model state vectors
• U_prepoststep: The name of a user supplied routine that is called before and after the analysis step. Here the user has the possibility to access the state ensemble and can e.g. compute estimated variances or can write the ensemble states the state estimate into files.
• status: The integer status flag. It is zero, if PDAF_get_state is exited without errors.

PDAF also has a Simplified Interface providing the routine PDAF_get_state_si. In the simplified interface, the names of all user-supplied call back routines are predefined such that they not appear in the call to PDAF_get_state_si. More information on the pre-defined names is provided in the documentation of PDAF's simplified interface.

PDAF_put_state_X

There is a separate routine PDAF_put_state_X for each of the filter algorithms. The name of the routine includes the name of the filter at its end (instead of X). The purpose of the PDAF_put_state_X routines is to write back the forecast model fields into the array holding the ensemble of model state vectors. In addition, the routine checks if the current forecast phase is completed. If not, the routine is exited and the next cycle of the ensemble loop is performed. If the current forecast phase is completed, the routine executes the analysis step of the chosen filter algorithm. The interface to each put-state routine is specific for each filter algorithm, because the names of several user-supplied routines have to be specified, which are specific for each filter algorithm. However, at the stage of implementing the ensemble integration only the first and last arguments of the routines are relevant.

For example, the interface when using the SEIK filter is the following:

  SUBROUTINE PDAF_put_state_seik(U_collect_state, U_init_dim_obs, U_obs_op, &
                                 U_init_obs, U_prepoststep, U_prodRinvA, U_init_obsvar, status)

At this state of the implementation only these arguments are relevant:

• U_collect_state: The name of the user-supplied routine that initializes a state vector from the array holding the ensemble of model states from the model fields. This is basically the inverse operation to U_dist_state used in PDAF_get_state
• status: The integer status flag. It is zero, if PDAF_get_state is exited without errors.

The other arguments are names of user-supplied subroutines that are only executed if the analysis step is executed (See the section Compilation and testing for how to provide these routines for compilation at this stage). These routines are explained in the next section of the implementation guide (Implementation of the Analysis step) separately for each available filter algorithm.

PDAF also has a Simplified Interface providing the routine PDAF_out_state_X_si. In the simplified interface, the names of all user-supplied call back routines are predefined such that they not appear in the call to PDAF_put_state_X_si. More information on the pre-defined names is provided in the documentation of PDAF's simplified interface.

User-supplied routines

Here, only the user-supplied routines are discussed that are required at this stage of the implementation (that is, the ensemble integration). For testing (see Compilation and testing), all routines need to exist, but only those described here in detail need to be implemented with functionality.

To indicate user-supplied routines we use the prefix U_. In the template directory templates/ as well as in the example implementation in testsuite/src/dummymodel_1D these routines exist without the prefix, but with the extension _pdaf.F90. In the section titles below we provide the name of the template file in parentheses.

U_next_observation (next_observation_pdaf.F90)

The interface for this routine is

SUBROUTINE next_observation(stepnow, nsteps, doexit, timenow)

  INTEGER, INTENT(in)  :: stepnow  ! Number of the current time step
  INTEGER, INTENT(out) :: nsteps   ! Number of time steps until next obs
  INTEGER, INTENT(out) :: doexit   ! Whether to exit forecasting (1 for exit)
  REAL, INTENT(out)    :: timenow  ! Current model (physical) time

The routine is called once at the beginning of each forecast phase. It is executed by all processes that participate in the model integrations.

Based on the information of the current time step, the routine has to define the number of time steps nsteps for the next forecast phase. In addition, the flag doexit has to be initialized to provide the information if the external ensemble loop can be exited. timenow is the current model time. This variable should also be initialized. It is particularly important, if an ensemble task integrates more than one model state. In this case timenow can be used to correctly jump back in time.

Some hints:

• If the time interval between successive observations is known, nsteps can be simply initialized by dividing the time interval by the size of the time step
• doexit should be 0 to continue the assimilation process. In most cases doexit is set to 1, when PDAF_get_state is called after the last analysis for which observations are available.
• At the first call to U_next_obs the variable timenow should be initialized with the current model time. At the next call a forecast phase has been completed. Thus, the new value of timenow follows from the timer interval for the previous forecast phase.

U_distribute_state (distribute_state_pdaf.F90)

The interface for this routine is

SUBROUTINE distribute_state(dim_p, state_p)

  INTEGER, INTENT(in) :: dim_p           ! State dimension for PE-local model sub-domain
  REAL, INTENT(inout) :: state_p(dim_p)  ! State vector for PE-local model sub-domain

This routine is called during the forecast phase as many times as there are states to be integrated by a model task. Again, the routine is executed by all processes that belong to model tasks.

When the routine is called a state vector state_p and its size dim_p are provided. As the user has defined how the model fields are stored in the state vector, one can initialize the model fields from this information. If the model is not parallelized, state_p will contain a full state vector. If the model is parallelized using domain decomposition, state_p will contain the part of the state vector that corresponds to the model sub-domain for the calling process.

Some hints:

• If the state vector does not include all model fields, it can be useful to keep a separate array to store those additional fields. This array has to be kept separate from PDAF, but can be defined using a module like mod_assimilation.

U_prepoststep (prepoststep_ens_pdaf.F90)

The interface of the routine is identical for all filters. However, the particular operations that are performed in the routine can be specific for each filter algorithm. Here, we exemplify the interface on the example of the SEIK filter.

The interface for this routine is

SUBROUTINE prepoststep(step, dim_p, dim_ens, dim_ens_p, dim_obs_p, &
                       state_p, Uinv, ens_p, flag)

  INTEGER, INTENT(in) :: step        ! Current time step
                         ! (When the routine is called before the analysis -step is provided.)
  INTEGER, INTENT(in) :: dim_p       ! PE-local state dimension
  INTEGER, INTENT(in) :: dim_ens     ! Size of state ensemble
  INTEGER, INTENT(in) :: dim_ens_p   ! PE-local size of ensemble
  INTEGER, INTENT(in) :: dim_obs_p   ! PE-local dimension of observation vector
  REAL, INTENT(inout) :: state_p(dim_p) ! PE-local forecast/analysis state
                                     ! The array 'state_p' is not generally not initialized in the case of SEIK/EnKF/ETKF.
                                     ! It can be used freely in this routine.
  REAL, INTENT(inout) :: Uinv(dim_ens-1, dim_ens-1) ! Inverse of matrix U
  REAL, INTENT(inout) :: ens_p(dim_p, dim_ens)      ! PE-local state ensemble
  INTEGER, INTENT(in) :: flag        ! PDAF status flag

The routine U_prepoststep is called once at the beginning of the assimilation process. In addition, it is called during the assimilation cycles before the analysis step and after the ensemble transformation. The routine is called by all filter processes (that is filterpe=1).

The routine provides for the user the full access to the ensemble of model states. Thus, user-controlled pre- and post-step operations can be performed. For example the forecast and the analysis states and ensemble covariance matrix can be analyzed, e.g. by computing the estimated variances. If the smoother is used, also the smoothed ensembles can be analyzed. In addition, the estimates can be written to disk.

Hint:

• If a user considers to perform adjustments to the estimates (e.g. for balances), this routine is the right place for it.
• Only for the SEEK filter the state vector (state_p) is initialized. For all other filters, the array is allocated, but it can be used freely during the execution of U_prepoststep.
• The interface through which U_prepoststep is called does not include the array of smoothed ensembles. In order to access the smoother ensemble array one has to set a pointer to it using a call to the routine PDAF_get_smootherens (see page on auxiliary routines)

U_collect_state (collect_state_pdaf.F90)

The interface for this routine is

SUBROUTINE collect_state(dim_p, state_p)

  INTEGER, INTENT(in) :: dim_p           ! State dimension for PE-local model sub-domain
  REAL, INTENT(inout) :: state_p(dim_p)  ! State vector for PE-local model sub-domain

This routine is called during the forecast phase as many times as there are states to be integrated by a model task. It is called at the end of the integration of a member state of the ensemble. The routine is executed by all processes that belong to model tasks.

When the routine is called, a state vector state_p and its size dim_p are provided. The operation to be performed in this routine is inverse to that of the routine U_distribute_state. That is, the state vector state_p has to be initialized from the model fields. If the model is not parallelized, state_p will contain a full state vector. If the model is parallelized using domain decomposition, state_p will contain the part of the state vector that corresponds to the model sub-domain for the calling process.

Some hints:

• If the state vector does not include all model fields, it can be useful to keep a separate array to store those additional fields. This array has to be kept separate from PDAF, but can be defined using a module like mod_assimilation.

Simulating model errors

The implementation of the filter algorithms does not support the specification of a model error covariance matrix. This was left out, because in the SEEK and SEIK filter, the handling can be extremely costly, as the model error covariance matrix has to be projected onto the ensemble space. Instead PDAF support the simulation of model errors by disturbing fields during the model integration. For this, some routine will be required that is inserted into the time stepping loop of the model. As this procedure is specific to each model, the is no routine provided by PDAF for this.

Compilation and testing

To compile the extended model code with PDAF, one has to extend the Makefile for the model by adding the additional user-supplied routines. While all of the user-supplied routines need to exist not all of them need to be fully implemented at this time if the following procedure is used. The routines that will not be called are U_init_dim_obs, U_obs_op, U_init_obs, U_prodRinvA, U_init_obsvar. A simple way to provide them for the compilation could be to copy the corresponding files (i.e. named without U_) from the template directory templates/ and to include these files in the compilation and linking. These templates are simple stubs without any functionality.

At this implementation stage one can use the preprocessor definition PDAF_NO_UPDATE (available from Version 1.6.1). With this, the actual analysis step of the chosen filter algorithm is not executed. Accordingly, only the user-supplied routines used in PDAF_get_state as well as the routine U_collect_state need to be implemented with functionality. The other routines will not be executed, because they are only called during the analysis step. Generally with PDAF_NO_UPDATE the program performs just an ensemble integration. That is, PDAF is initialized by PDAF_init. Then a forecast is computed by using PDAF_get_state and the chosen PDAF_put_state_* routine. At the initial time U_prepoststep is executed by PDAF_get_state. U_next_obs will provide the number of time steps to be computed by the model and U_distributed_state will initialize the model fields. Subsequently the ensemble integration is performed and the forecast fields are written back to the ensemble array by U_collect_state. Upon completion of the forecast phase, the routine U_prepoststep is executed twice. The first time is the regular call before the analysis is executed. Thus, it allows to access the forecast ensemble. If the analysis would not be deactivated, the second call to U_prepoststep would be after the analysis allowing access to the ensemble directly after the analysis. As the analysis is deactivated here, the ensemble will be the same as in the first call.

This test allows to check the following:

• Is U_prepoststep working correctly?
• Does U_next_observation work correctly and is the information from this routine used correctly for the model integration
• Are U_distribute_state and U_collect_state work correctly?

One could also comment out the actual time stepping part of the model. This would allow to only test the interfacing between PDAF and the model.

It is important to ensure that the ensemble integration performs correctly. The simplest case should be a parallel configuration in which the number of model tasks equals the ensemble size as here the model tasks always compute forward in time. If the number of model tasks is smaller than the ensemble size, some model tasks will have to integrate multiple states of the ensemble. If a model task has to integrate two states, the model will have to jump back in time for the integration of the second state. It might be that some arrays of the model need to be re-initialized to ensure that the second integration is consistent. Also, one might need to check if the initialization of forcing fields (e.g. wind stress over the ocean) performs correctly for the second integration. (Sometimes model are implemented with the constraint that the model time always increases, which is the normal case for pure model simulations without assimilation.) A useful test is to initialize an ensemble in which all states are equal. If this ensemble is integrated the forecast states of the ensemble should, of course, still be equal.